OpenCV線性代數-cvSVBkSb奇異值倒回替代法

cvSVBkSb()為解線性系統解專用的,實際上它跟前面的cvSolve()的線性系統求解的奇異值法是一樣的東西,cvSolve()內部的CV_SVD參數它的計算方式實際上就是呼叫cvSVBkSb()這個函式,所以,用起來的方式差不多,在這邊簡單的做cvSVBkSb()的使用方法.


線性系統求解-奇異值倒回替代法
#include <cv.h>
#include <highgui.h>
#include <stdio.h>

void PrintMatrix(CvMat *Matrix,int Rows,int Cols);

float Array1[]={-1,2,-1,3,1,-4,5,-5,-2,6,-5,7,-1,-4,11,-2};
float Array2[]={6,-7,7,7};
int main()
{
    CvMat *A=cvCreateMat(4,4,CV_32FC1);
    CvMat *b=cvCreateMat(4,1,CV_32FC1);
    CvMat *W=cvCreateMat(4,4,CV_32FC1);
    CvMat *U=cvCreateMat(4,4,CV_32FC1);
    CvMat *V=cvCreateMat(4,4,CV_32FC1);
    CvMat *x=cvCreateMat(4,1,CV_32FC1);

    cvSetData(A,Array1,A->step);
    cvSetData(b,Array2,b->step);
    cvSVD(A,W,U,V);
    cvSVBkSb(W,U,V,b,x,0);

    PrintMatrix(x,x->rows,x->cols);
    system("pause");
}
void PrintMatrix(CvMat *Matrix,int Rows,int Cols)
{
    for(int i=0;i<Rows;i++)
    {
        for(int j=0;j<Cols;j++)
        {
            printf("%.2f ",cvGet2D(Matrix,i,j).val[0]);
        }
        printf("\n");
    }
}

在這邊,要用cvSVBkSb()之前就要先用到前面的cvSVD()了,在將cvSVD()奇異值分解的數值餵進cvSVBkSb()裡面解線性系統解,這邊奇異值倒回替代法用的是虛反矩陣的觀念,虛反矩陣則是在前面cvInvert()裡面有提到,而它的第四個引數為cvSVBkSb()的參數及代號,與cvSVD()相同,可輸入的參數為

#define CV_SVD_U_T 2
#define CV_SVD_V_T 4

分別代表U矩陣跟V矩陣輸入是否為轉置,如果不需要任何轉置輸入則將參數代號預設為0,而此題的線性系統,驗證及計算的方式如下










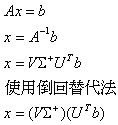
cvSVBkSb()
為線性系統求解的奇異值替代倒回法,對於一個無解的線性系統,使用奇異值替代倒回法可以求得近似解,但是使用cvSVBkSb()這個函式時必須要先做cvSVD()奇異值分解的計算,在將分解後的矩陣丟給cvSVBkSb()求線性系統的解,使用到的是虛反矩陣的概念,第一個引數為CvMat結構的W矩陣,第二個引數為CvMat結構的U矩陣,第三個引數為CvMat結構的V矩陣,前面的矩陣結構都必須經由cvSVD()奇異值分解計算而得,第四個引數為Ax的線性組合數據,第五個引數為x的解集合,第六個引數則是cvSVBkSb()的參數輸入,只有CV_SVD_U_T及CV_SVD_V_T或者是0(無參數)這三種.
cvSVBkSb(CvMat資料結構W矩陣輸入,CvMat資料結構U矩陣輸入,CvMat資料結構V矩陣輸入,CvMat資料結構b矩陣輸入,CvMat資料結構線性系統解集合x矩陣,目標參數或代號)